Solution des jeux de PM38

Cherchez l'erreur

Souvenez-vous du cours de logique et des tables de vérité appliquées aux implications « A ⇒ B »: lorsque la valeur de la prémisse A vaut 0, c'est-à-dire lorsque la prémisse est fausse, l'implication est toujours vraie. La propriété de symétrie dit que l'implication « xℛy ⇒ yℛx » est vraie, mais cela ne présage en rien que xℛy soit vrai; cela dit seulement que si xℛy est vrai, alors yℛx est vrai.

Examinons un exemple, pioché dans l'ouvrage Les contre-exemples en mathématiques: dans ℤ, xℛy si xy > 0. La relation est à l'évidence symétrique, et elle est transitive car si xy > 0 et si yz > 0 alors xy²z > 0 donc y n'est pas nul puis xz > 0. Cependant, elle n'est pas réflexive car 0 n'est pas en relation avec lui-même.

L'implication « 0ℛy => yℛ0 » est vraie d'un point de vue logique, puisque son hypothèse 0ℛy est fausse. Mais 0 n'est en relation avec personne.

L'hypothèse de réflexivité est donc nécessaire dans la définition d'une relation d'équivalence.

Culture mathématique

• sqrt(pi) / 2.
• Les suites de Cauchy, l'inégalité de Cauchy-Schwarz, le critère de convergence de Cauchy pour les séries entières, le produit de Cauchy de deux séries, le théorème de Cauchy-Lipschitz pour les équations différentielles...
• Le symbole « delta » indicé par deux entiers i et j, qui vaut 1 si i=j, 0 sinon.
• La factorielle.
• L'écriture en « petit o(x) » désigne une fonction qui est négligeable devant x au voisinage de 0. L'écriture « grand O(x²) » désigne une fonction dont le quotient par x² est borné au voisinage de 0. Cette deuxième écriture est plus précise: si une fonction vérifie « g(x)/x² est borné en 0 », alors à l'évidence « g(x)/x tend vers 0 en 0 ». La réciproque est fausse: il suffit de considérer la fonction g(x) = x^3/2.
  L'écriture en « grand O » apporte plus d'informations que l'écriture en « petit o ». Lorsque l'on calcule des développements limités ou asymptotiques à partir de fonctions usuelles (de DL connu), il est préférable de partir de la version « grand O » de leurs DL.

La balance

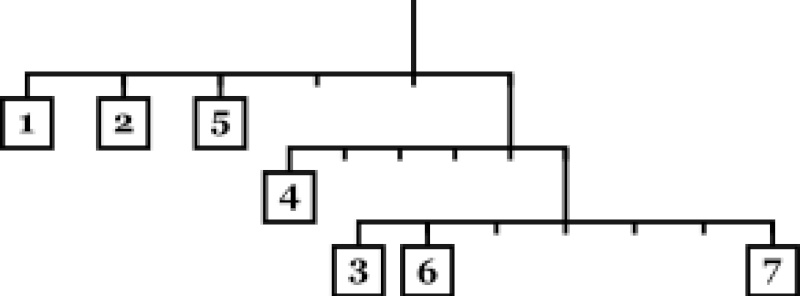
Énigmes

1. 
   
2. La méthode simple: on met 4 pièces sur chaque plateau, on regarde quel côté est le plus léger; on répartit ensuite ces 4 pièces en 2 paquets de 2, et on regarde de nouveau quel côté est le plus léger. Il suffit, dans un troisième temps, de peser les deux pièces de ce dernier paquet.
   On peut aussi s'en sortir en deux pesées: mettons 3 pièces sur chacun des plateaux. S'ils sont à l'équilibre, il suffit de peser les deux dernières pièces. Sinon, il reste à déterminer quelle est la pièce légère dans un paquet de 3. On en pèse deux choisies au hasard: si la balance penche, on a fini; sinon, la pièce recherchée est celle qui n'est pas sur la balance.
3. 
   
4. Lorsque l'on interroge les enfants, on se limite aux familles qui ont des enfants.
5. Considérons la tirelire portant l'étiquette « 1 billet de 10 et 1 billet de 20 »: puisque les étiquettes ne correspondent jamais au contenu, on est sûr que cette tirelire contient soit deux billets de 10, soit deux billets de 20, ce que l'on tranche en regardant l'un de ses billets. Les deux cas étant symétriques, on peut supposer sans perdre en généralité que l'on tire un billet de 10. On a donc identifié la tirelire contenant deux billets de 10.
   
   Il reste deux tirelires. Considérons celle dont l'étiquette indique « 2 billets de 20 ». On déjà est sûr qu'elle ne contient pas 2 billets de 20. Elle ne peut pas non plus contenir 2 billets de 10 puisque cette tirelire a déjà été identifiée. Elle contient donc 1 billet de 10 et 1 billet de 20, et la dernière contient 2 billets de 20.
   
   Cette énigme n'est pas aussi difficile qu'il y paraît car il n'y a que deux manières de déplacer les étiquettes de telle sorte qu'aucune ne corresponde au contenu de la tirelire; elles correspondent aux permutations circulaires sur un ensemble à trois éléments.
6. Le premier aller embarque 5 personnes et en ramène 1: restent 4 personnes sur la rive, et 9 minutes sont écoulées. De même, le deuxième aller-retour amène 4 nouvelles personnes sur la rive opposée, et 18 minutes sont écoulées. On ne peut pas réaliser de troisième aller-retour, mais on peut faire un dernier voyage aller, qui ajoute 5 personnes au groupe déplacé. Au total, 13 personnes arriveront donc à temps pour le spectacle.

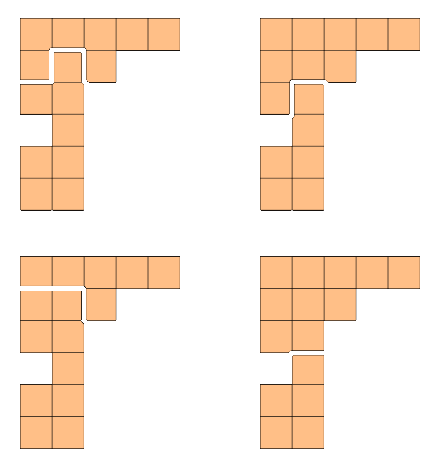
Logimages et sudokus